ДВИЖЕНИЕ САМОЛЕТА ПРИ БОЛЬШИХ УГЛОВЫХ СКОРОСТЯХ ВРАЩЕНИЯ ОТНОСИТЕЛЬНО ПРОДОЛЬНОЙ оси

Как было показано ранее, можно выделить три основ­ные области значений угловой скорости крена со* — малые, про­межуточные и большие, в каждой из которых движение самолета обладает своими особенностями. При малых угловых скоростях крена в уравнениях движения можно опустить инерционные члены и рассматривать их как линейные уравнения, учитывая, если это необходимо, только нелинейности аэродинамических коэффициен­тов. Наиболее сложные закономерности имеет управляемое дви­жение самолета, сопровождающееся угловыми скоростями крена, при которых инерционные и аэродинамические моменты имеют одинаковый порядок величин; это область угловых скоростей крена, которая главным образом и рассматривается в настоящей книге. И, наконец, имеется область очень больших угловых ско­ростей крена, которая характерна тем, что инерционные моменты гироскопической устойчивости самолета при движении с такими угловыми скоростями превосходят моменты аэродинамической устойчивости. Такое движение является в некотором смысле предельным движением самолета при маневре крена и резуль­таты, полученные при его исследовании, помогают анализировать некоторые виды движения самолета при больших угловых скоро­стях крена.

Итак, большими значениями угловой скорости со* можно считать такие, для которых выполняется неравенство

со* > max (соа, соэ).

Когда большей критической скоростью крена является ве­личина соа, неравенство (11.1) может быть переписано в размер­ном виде следующим образом:

(1у — /л) Ых> — trizqSbA. ■ (11.2)

Неравенство (11.2) означает, что основное влияние на движение самолета будут оказывать инерционные моменты, по сравнению с которыми влияние аэродинамических моментов устойчивости мало и ими можно пренебречь. Учитывая малость аэродинамиче­ских моментов устойчивости по сравнению с инерционными, с помощью формул табл. 9.1 легко показать, что статические ре­шения при | йх | -> оо стремятся к следующим предельным зна­чениям:

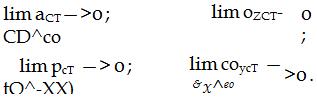(11.3)

При этом соотношения (11.3) выполняются при любых отклоне­ниях стабилизатора и руля направления, что объясняется большой гироскопической устойчивостью движения самолета.

Подставляя выражения (11.3) в уравнения движения самолета

(3.13) в качестве параметров невозмущенного движения, линеари­зуем их и получим уравнения в вариациях относительно движе­ния, заключающегося в быстром вращении самолета относительно продольной оси с угловой скоростью крена (ох = Q:

u>z + = т^б сог;

== rn*yv<s)y

а’ + |ЛЙ|3 -f — Ц — а = |UDZ; СР

Р’ — ЦЙа—— |~Р = !-1сог/>

со* — nixxсо* = т*р. (11.6)

Нетрудно видеть, что уравнения разделились на две пары линейных уравнений второго порядка и одно уравнение первого порядка, которые могут решаться последовательно. Решение уравнений (11.4) не зависит от остальных уравнений и может быть записано в следующем виде:

со,, == Аг^х -f — А2^%

coz — BteKiT — j — B2eKzX-

Случай больших угловых скоростей крена

Комплексно-сопряженные корни %.2 удобно определять С ПО­МОЩЬЮ приближенной формулы, основанной на допущении о ма­лости коэффициентов демпфирования по сравнению с мнимой частью корня:

h. 2 ^ ~ (тГб + thyy] ±/uQ [ АВ. (11.8)

Остальные корни системы уравнений (11.4)—(11.6) при аналогич­ных допущениях приближенно можно записать в виде I 1 С<Н С? Ц 2 + (11.9) X. = mG)*. 0 X (11.10)

Уравнения (11.5) и (11.6) являются однородными линейными уравнениями относительно переменных а, р и wv, поскольку решения для Соу и <Ь2 известны (11.7). Решения для аир зависят от изменения вариаций угловых скоростей йу, со2 в процессе движения, благодаря чему и решение для вариации со* также зависит от вариаций <ЬУ и 6з2. Таким образом, решение для со£/ и ш2 зависит от двух корней характеристического уравнения и двух констант, определяемых начальными условиями; решение для а и р в общем случае произвольных начальных условий зависит от четырех корней и четырех констант, а решение для со* уже зависит от всех пяти корней и пяти констант. Дальнейшее упрощение анализа возмущенного движения самолета может

быть получено, если рассматривать случай, когда га* = 0.

Проанализируем этот случай более подробно, рассматривая движение в фазовом пространстве угловых скоростей. Из уравне­ния оке) получим общее решение для со,:

сог = соЛ.0е?*т. (11.11)

Подставляя в решение (11.7) выражения для корней, преобразуем соотношение для <Ьу и <а2 к виду

— ЇГ ("1<1/ + tn^y} X і —т—

со,,е 2 ‘ гС у ‘ = Сд sin (pQ I А В) т;

(11-12)

1 ~®у~ __

о)2е 2 ‘ 26 шу ‘т — с21 sin(pQ I АВ) т + с22 cos (tiQ v АВ) т.

Из выражения (11.12), производя простые выкладки, получим

Введем новые переменные, связанные линейными зависимостями с угловыми скоростями и со2:

Си
= со
(П.14)
(	С’21 Си	с22
C^Zl*

Произведя замену переменных (11.14) в соотношениях (11.13), возведем в квадрат каждое из этих соотношений и сложим их. В итоге получим уравнения интегральных кривых в фазовом про­странстве для переменных со<д, соп:

-2 —2 (т®?+го“*Л Т

©и + cof, = eV <б У ) . (11.15)

Исключая время из соотношения (11.15) с помощью решения для со, (11.11), получим уравнение семейства поверхностей в фазовом пространстве, на которых лежат интегральные кривые:

-2 -2 ~

С0^1 <0*1 = Cq (Ох * > (11.16)

_С0_ _Сй,.

— т z т У

Со = «Ло * " . (11.17)

При каждом значении коэффициента с0 поверхность, описы­ваемая уравнением (11.16), представляет собой тело вращения относительно оси Ocov. Если решения ДЛЯ G),rl, G)zl, со, устойчивы, то движение в фазовом пространстве происходит по поверхности параболоида, касающегося начала координат:

СО, — СО*д сод 0.

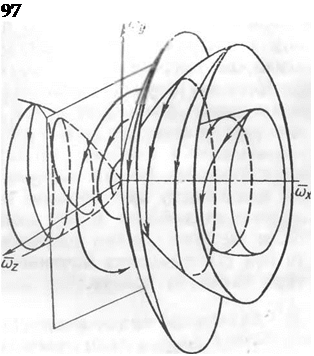
Схема движения в фазовом пространстве показана на рис. 11.1. Система уравнений движения (11.4)—(11.6) имеет один действи­тельный корень (11.10), определяющий сепаратрисную поверх­ность, уравнение которой непосредственно следует из решения для со, (11.11):

со, = 0. (11.19)

Движение в сепаратрисной плоскости будет устойчивым, если т®х < 0, и неустойчивым, если т^х > 0. Движение в фазовом

пространстве действительных угловых скоростей со,, сог, о), имеет те же особенности, что и движение в пространстве пере­менных ыу19 со21, со,. Отличие состоит в том, что если в простран­стве со, д, 0)21, со, сечение поверхности, по которой движется фигу-

www. vokb-la. spb. ru — Самолёт своими руками

Сл>ЧаЙ больших угловых скоростей крена

Рис. 11.1. Фазовая картина движения в окрестности особой точки, соответ­ствующей быстрому вращению самоле­та по крену ративная точка, плоскостью ор­тогональной оси 0(ЬХ является кругом, то в пространстве со7, со., соЛ. такое сечение — эллипс.

Изменение углов атаки и скольжения самолета в возму­щенном движении описывается уравнениями (11.5). Рассмотрим в первую очередь движение са­молета при наличии начальных возмущений только по углам атаки и скольжения, т. е. когда б)/у (0) = сог (0) = 0. Такое возму­щение можно представить как действие на самолет ступенчатого порыва ветра. Из выражений (11.4) следует, что угловые ско­рости <Ьу и coz остаются тождественно равными нулю, т. е. про­дольная ось самолета в возмущенном движении сохраняет по­стоянную ориентацию относительно инерциального пространства и может перемещаться только путем плоскопараллельного дви­жения, что объясняется большой гироскопической устойчивостью. Поскольку оЬу = со, = 0, уравнения (11.5) могут быть переписа­ны в более простом виде

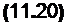а’ + uQp — f Ц — а = 0; СР

Р’ — |Л 9-а 1- р = 0.

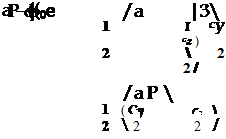Решение уравнений (11.20) при соответствующем выборе начала отсчета времени можно записать следующим образом:

Из выражений (11.21) видно, что решение для аир представляет собой колебательный затухающий процесс. Колебательный ха­рактер изменения углов а и Р обусловливается их кинематической связью с углом между продольной осью самолета и вектором ско­рости. Кроме этого, благодаря действию аэродинамической силы

4 Бюшгенс Г. С.

Приложение качественной теории дифференциальных уравнений

самолет начинает «сноситься» по потоку, и угол между неподвиж­ной в инерциальном пространстве осью вращения самолета и вектором скорости уменьшается.

Частные случаи движения ^быстро^вращающегося самолета показывают, что наблюдаются два типа движений, возникновение которых зависит от действующих возмущений. Если на быстро вращающийся самолет действуют^возмущения по углам в атаки и скольжения, то его возмущенное движение сводится к такому их изменению, при котором продольная ось самолета движется плоскопараллельно и не изменяет своей угловой ориентации. Если же возмущения приводят к изменению угловой скорости, то ось ОХ самолета начинает прецессировать относительно век­тора скорости полета.